Dragon Fury - CTF Challenge Write-up
Challenge Description
The challenge, titled "Dragon Fury," involved simulating a battle by computing the total damage dealt by dragons over successive rounds. The input consisted of two parts: a string representing a list of subarrays (each subarray containing possible damage values for a round) and an integer $T$ representing the target total damage. The objective was to select exactly one number from each subarray such that their sum equals $T$, and then output this combination as a list. We were guaranteed that there would be exactly one valid solution.
Solution
The provided Python code uses a backtracking approach to find the combination of damage values that sums to the target.
Code
from ast import literal_eval
def find_combination(subarrays, target):
def backtrack(start, current_sum, current_combination):
if start == len(subarrays):
if current_sum == target:
return current_combination
return None
for num in subarrays[start]:
result = backtrack(start + 1, current_sum + num, current_combination + [num])
if result is not None:
return result
return None
return backtrack(0, 0,)
# Read the input
input_text = input()
subarrays = literal_eval(input_text)
T = int(input())
# Find and print the valid combination
result = find_combination(subarrays, T)
print(result)
Explanation
-
find_combination(subarrays, target)Function: This is the main function that takes the list of subarrays and the target sum as input. It initializes the backtracking process. -
backtrack(start, current_sum, current_combination)Function: This recursive function explores all possible combinations.
start: Keeps track of the index of the current subarray being considered.current_sum: Stores the sum of the numbers chosen so far.current_combination: A list containing the numbers chosen so far.- Base Case: When
startequals the total number of subarrays, it checks if thecurrent_summatches thetarget. If it does, thecurrent_combinationis returned as the solution. - Recursive Step: For each number in the current subarray (
subarrays[start]), the function recursively calls itself for the next subarray (start + 1), adding the current number to thecurrent_sumand thecurrent_combination. If a valid combination is found in the recursive call, it is immediately returned.
-
Input Reading: The code reads the input in two steps: first, it reads the string representing the list of subarrays and uses
ast.literal_evalto convert it into a Python list of lists. Second, it reads the integer target sum $T$. -
Finding and Printing the Result: The
find_combinationfunction is called to find the valid combination, and the result (a list of numbers) is printed to the standard output.
Flag
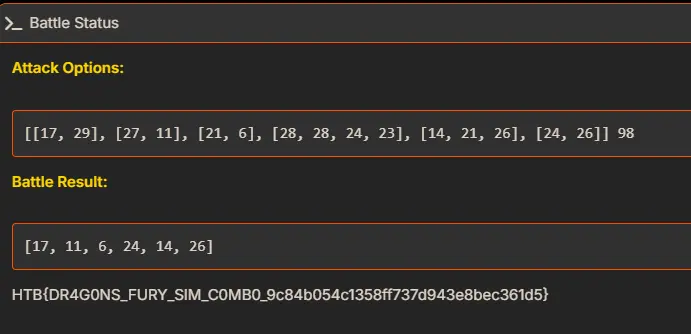
The solution to the challenge reveals the following flag:
HTB{DR4G0NS_FURY_SIM_C0MB0_9c84b054c1358ff737d943e8bec361d5}
